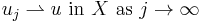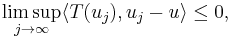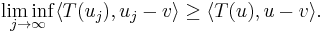Pseudo-monotone operator

In mathematics, a pseudo-monotone operator from a reflexive Banach space into its continuous dual space is one that is, in some sense, almost as well-behaved as a monotone operator. Many problems in the calculus of variations can be expressed using operators that are pseudo-monotone, and pseudo-monotonicity in turn implies the existence of solutions to these problems.

Definition

Let (X, || ||) be a reflexive Banach space. A linear map T : X → X^∗ from X into its continuous dual space X^∗ is said to be pseudo-monotone if T is a bounded linear operator and if whenever

$u_{j} \rightharpoonup u \mbox{ in } X \mbox{ as } j \to \infty$

(i.e. u_j converges weakly to u) and

$\limsup_{j \to \infty} \langle T(u_{j}), u_{j} - u \rangle \leq 0,$

it follows that, for all v ∈ X,

$\liminf_{j \to \infty} \langle T(u_{j}), u_{j} - v \rangle \geq \langle T(u), u - v \rangle.$

Properties of pseudo-monotone operators

Using a very similar proof to that of the Browder-Minty theorem, one can show the following:

Let (X, || ||) be a real, reflexive Banach space and suppose that T : X → X^∗ is continuous, coercive and pseudo-monotone. Then, for each continuous linear functional g ∈ X^∗, there exists a solution u ∈ X of the equation T(u) = g.

References

Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second edition ed.). New York: Springer-Verlag. pp. 367. ISBN 0-387-00444-0. (Definition 9.56, Theorem 9.57)